Section 4: Statistical Relationships

Sam Frederick

Columbia University

2/21/23

Today’s Section

• Correlation Coefficients

• Law of Large Numbers

• The Central Limit Theorem

• Hypothesis Testing

Correlation Coefficients

• Statistically summarize relationships between numeric variables

• Range from -1 to 1

• Values closer to -1 or 1 indicate stronger relationships

Correlation Coefficients

\(Cor(X, Y) = \frac{Cov(X,Y)}{\sqrt{Var(X)*Var(Y)}} = \frac{\frac{1}{n-1}\sum_{i=1}^n(X-\bar{X})(Y-\bar{Y})}{\sqrt{\frac{1}{n-1}\sum_{i=1}^n(X-\bar{X})^2 *\frac{1}{n-1} \sum_{i=1}^n(Y-\bar{Y})^2}}\)

Equivalently:

\(Cor(X,Y) = \frac{\sum_{i=1}^n (X-\bar{X})*(Y-\bar{Y})}{ \sqrt{\sum_{i=1}^n(X-\bar{X})^2 *\sum_{i=1}^n(Y-\bar{Y})^2}}\)

Correlation Coefficients in R

x <- c(1, 3, 5, 7, 9)
y <- c(1, 4, 7, 2 , 10)

• By hand:

numerator <- sum((x-mean(x))*(y - mean(y)))
denominator <- sqrt(sum((x-mean(x))^2)*sum((y - mean(y))^2))
round(numerator/denominator, 3)

[1] 0.683

• Using R functions:

round(cov(x, y)/sqrt(var(x)*var(y)), 3)

[1] 0.683

• Using one R function:

round(cor(x, y), 3)

[1] 0.683

Custom Functions in R

name <- function(arguments){
  tasks
  return(output)
}
name(arguments)

Custom Functions in R

square <- function(x) {
  return(x^2)
}
square(2)

[1] 4

square(4)

[1] 16

Custom Functions in R

correlation <- function(x, y) {
  numerator <- sum((x-mean(x))*(y - mean(y)))
  denominator <- sqrt(sum((x-mean(x))^2)*sum((y - mean(y))^2))
  return(round(numerator/denominator, 3))
}
correlation(x,y)

[1] 0.683

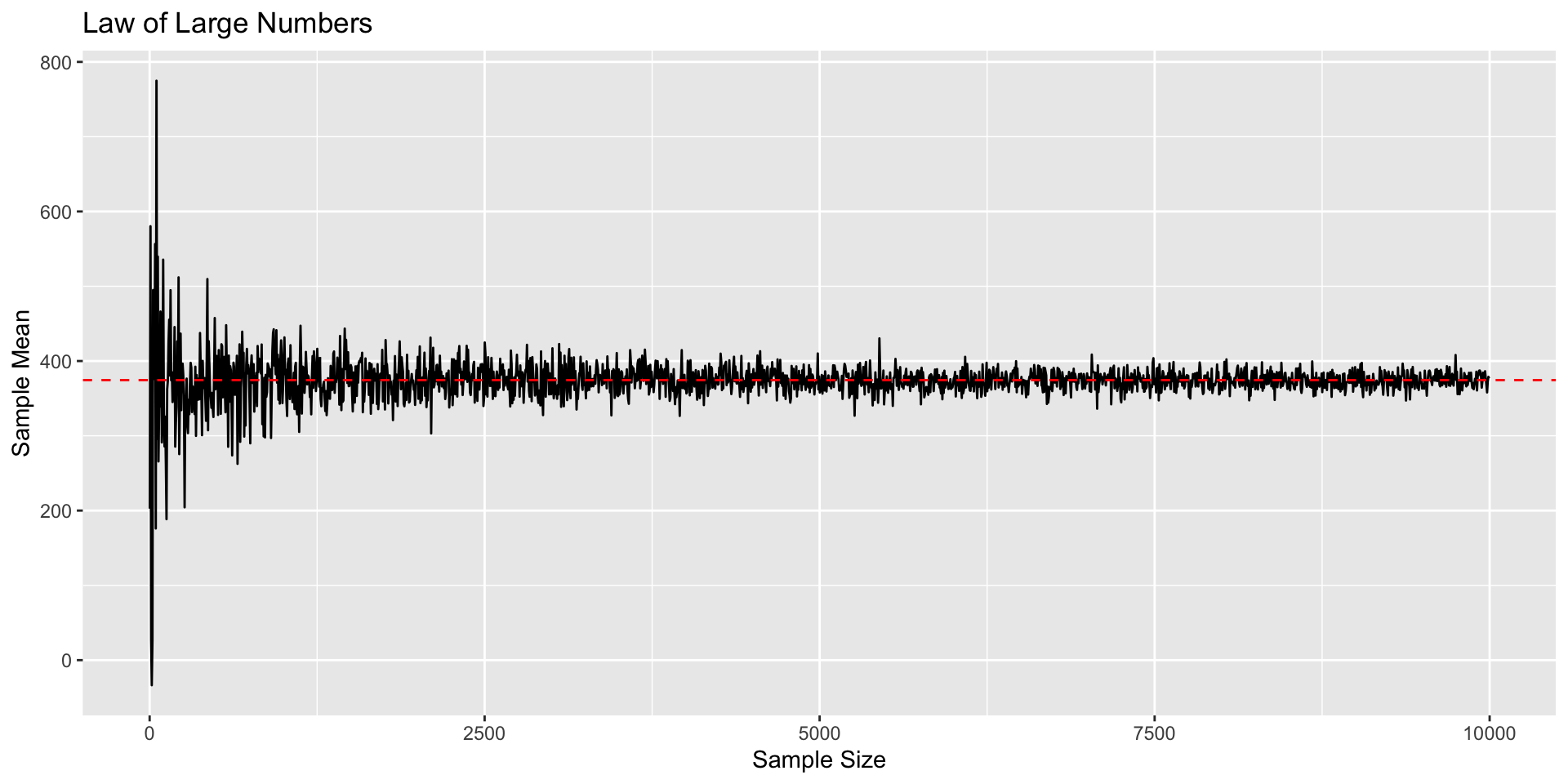
Law of Large Numbers

As \(n \to \infty\), sample mean approaches true population mean:

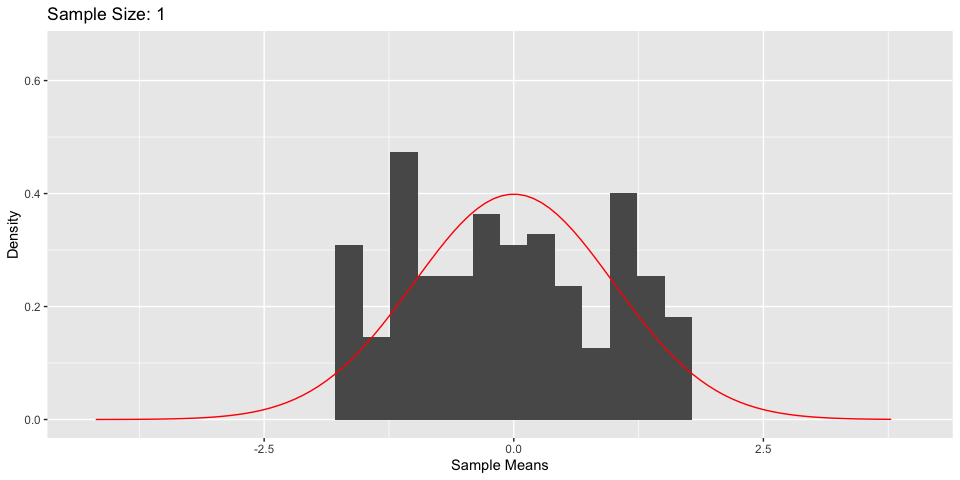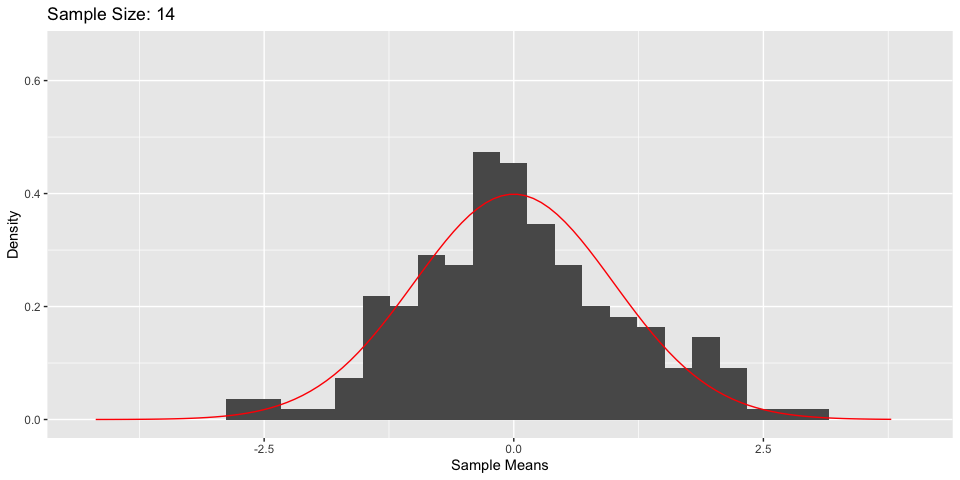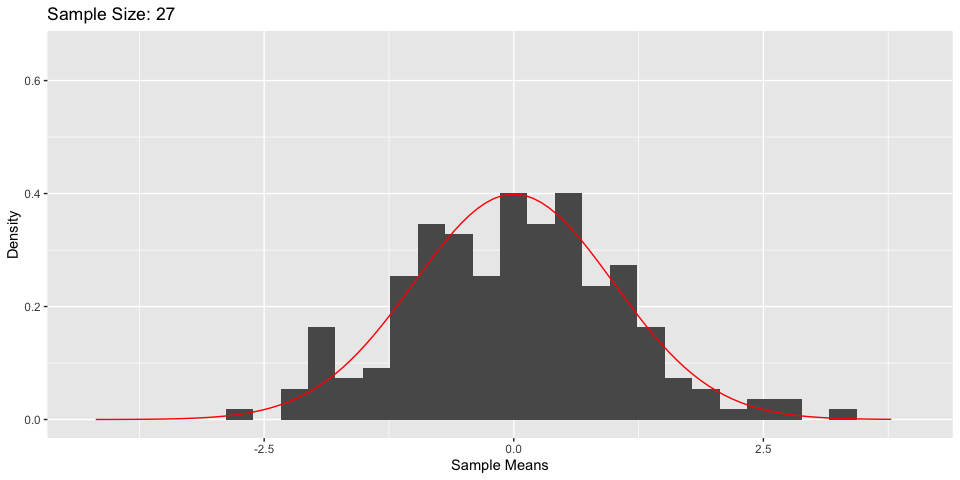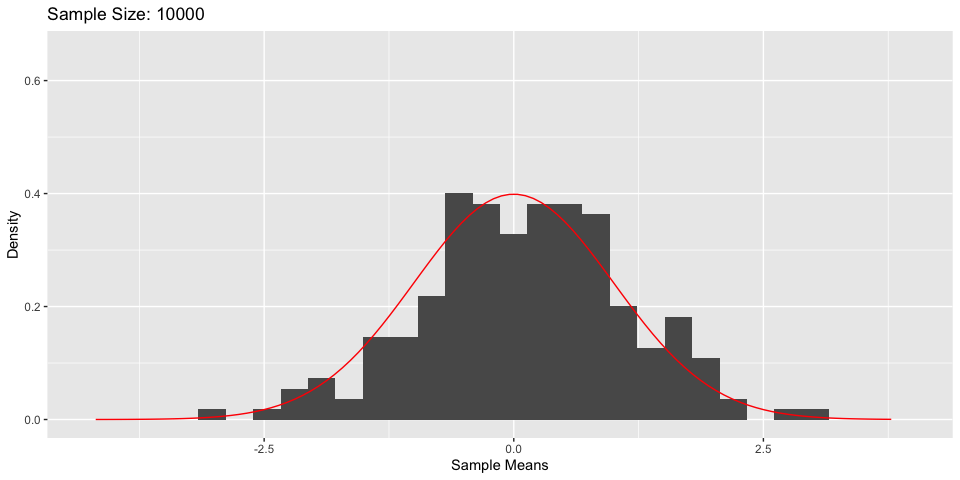
Central Limit Theorem

• As \(n \to \infty\), \(\sqrt{n}(\bar{X}_n-\mu) \to N(0, \sigma^2)\)

Central Limit Theorem

• What’s more, As \(n \to \infty\), \(\frac{\bar{X}_n - \mu}{\sigma/\sqrt{n}} \to N(0, 1)\)

Hypothesis Testing

• Null Hypothesis:
  • Usually that true population mean equal to some value (\(\mu = x\))
  • e.g., the true approval rate of Joe Biden is 50%
  • e.g., the difference between the conservatism of Democrats and Republicans is 0
• Alternative Hypothesis:
  • Two-sided: \(\mu \neq x\)
  • One-sided: \(\mu > x\) or \(\mu < x\)

Hypothesis Testing

• Calculate the Z-Score based on null hypothesis:
  • \(Z = \frac{\bar{X} - \mu_{0}}{\sigma/\sqrt{n}}\)
  • Two-Sample/Difference-in-Means Test:
    • \(Z = \frac{(\bar{X} - \bar{Y}) - (\mu_{0x}-\mu_{0y})}{\sqrt{\sigma_x^2/n_x + \sigma_y^2/n_y}}\)

Hypothesis Testing

• Under the Central Limit Theorem, the Z-Score should be
  • distributed approximately standard normal
    • if we repeated the sampling process many times with a large enough sample
    • and if the null hypothesis is true

Hypothesis Testing

• Standard Normal Distribution has known properties
  • Calculate probability of observing Z-Score at least as large as observed Z-Score
    • if the null hypothesis is true
  • This is the p-value

Hypothesis Testing: Example

nominate <- read_csv("~/Downloads/HSall_members.csv") %>%
  filter(congress==118&party_code%in%c(100, 200)&
           chamber!="President") 
dem <- nominate %>% filter(party_code==100) %>% drop_na(nominate_dim1)
rep <- nominate%>% filter(party_code==200) %>% drop_na(nominate_dim1)
diff_in_means <- mean(rep$nominate_dim1) - mean(dem$nominate_dim1)
denominator <- sqrt((var(rep$nominate_dim1, na.rm = T)/nrow(rep)) +
                      (var(dem$nominate_dim1)/nrow(dem)))
z_score <- diff_in_means/denominator
round(z_score, 3)

[1] 73.525

Hypothesis Testing: Example

ggplot()+
  stat_function(fun = dnorm) + 
  xlim(c(-3, 3)) + 
  labs(x = "X", y = "Density", 
       title = "Standard Normal Distribution")

Hypothesis Testing: Example

ggplot()+
  stat_function(fun = dnorm) + 
  xlim(c(-100,100)) + 
  labs(x = "X", y = "Density", 
       title = "Standard Normal Distribution") + 
  geom_vline(xintercept = z_score, color = "red", lty = "dashed")

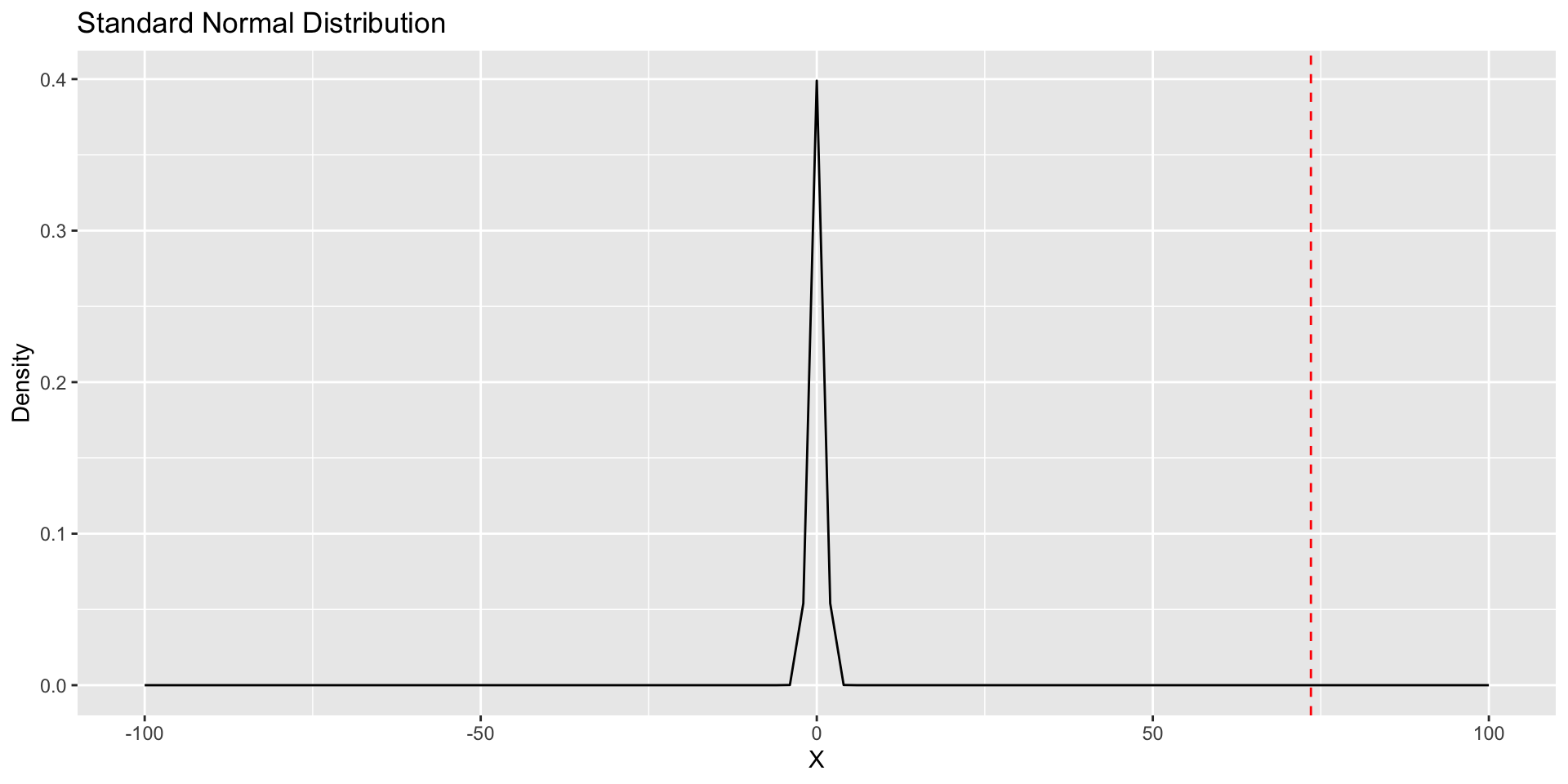
Hypothesis Testing: Example

• One-Sided Hypothesis Test: \(\mu_{0R} - \mu_{0D} >0\)

1-pnorm(z_score, mean = 0, sd = 1)

[1] 0

• Two-Sided Hypothesis Test: \(\mu_{0R}- \mu_{0D} \neq 0\)

2*(1-pnorm(z_score, mean = 0, sd = 1))

[1] 0

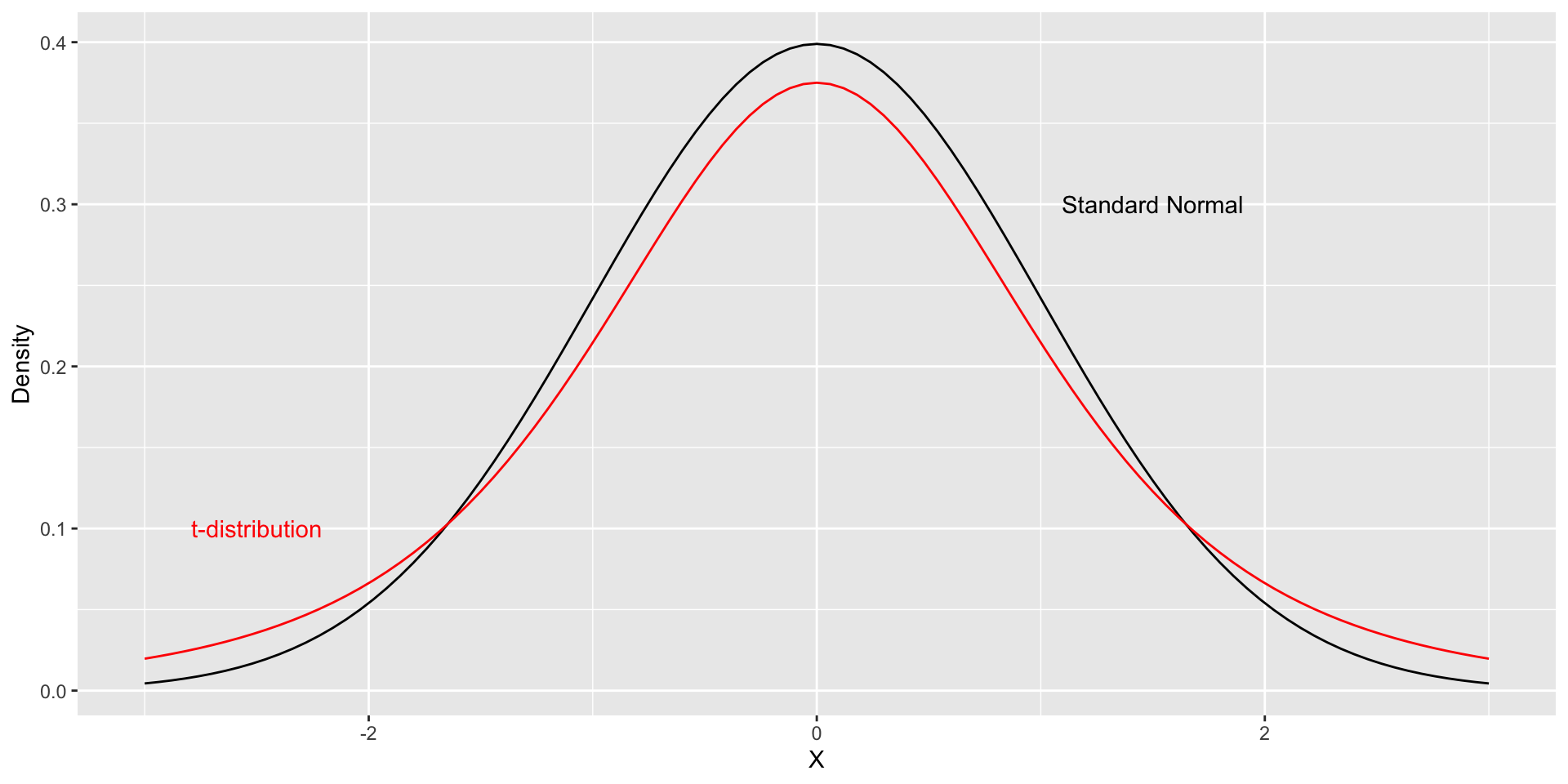
Hypothesis Testing: T-Distribution

• Often use the t distribution instead of normal distribution

  • especially with small sample sizes

• t-distribution places more probability in the tails

• In large samples, the t-distribution is equivalent to the normal distribution

T Distribution

Hypothesis Testing

• In R, can use the t.test() function

t.test(rep$nominate_dim1, dem$nominate_dim1)

    Welch Two Sample t-test

data:  rep$nominate_dim1 and dem$nominate_dim1
t = 73.525, df = 500.98, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 0.8825648 0.9310273
sample estimates:
 mean of x  mean of y 
 0.5222045 -0.3845916 

Confidence Intervals

• We often want some idea of uncertainty in our estimates

• Use Central Limit Theorem to construct “confidence intervals” around our estimates

• Lower End: sample estimate - \(qnorm(0.975)*\)Standard Error

• Upper End: sample estimate + \(qnorm(0.975)*\)Standard Error

Confidence Intervals: Example

dem_mean <- mean(dem$nominate_dim1)
dem_mean - qnorm(0.975)*sd(dem$nominate_dim1)/sqrt(nrow(dem))

[1] -0.399397

dem_mean

[1] -0.3845916

dem_mean + qnorm(0.975)*sd(dem$nominate_dim1)/sqrt(nrow(dem))

[1] -0.3697862

Confidence Intervals: Example

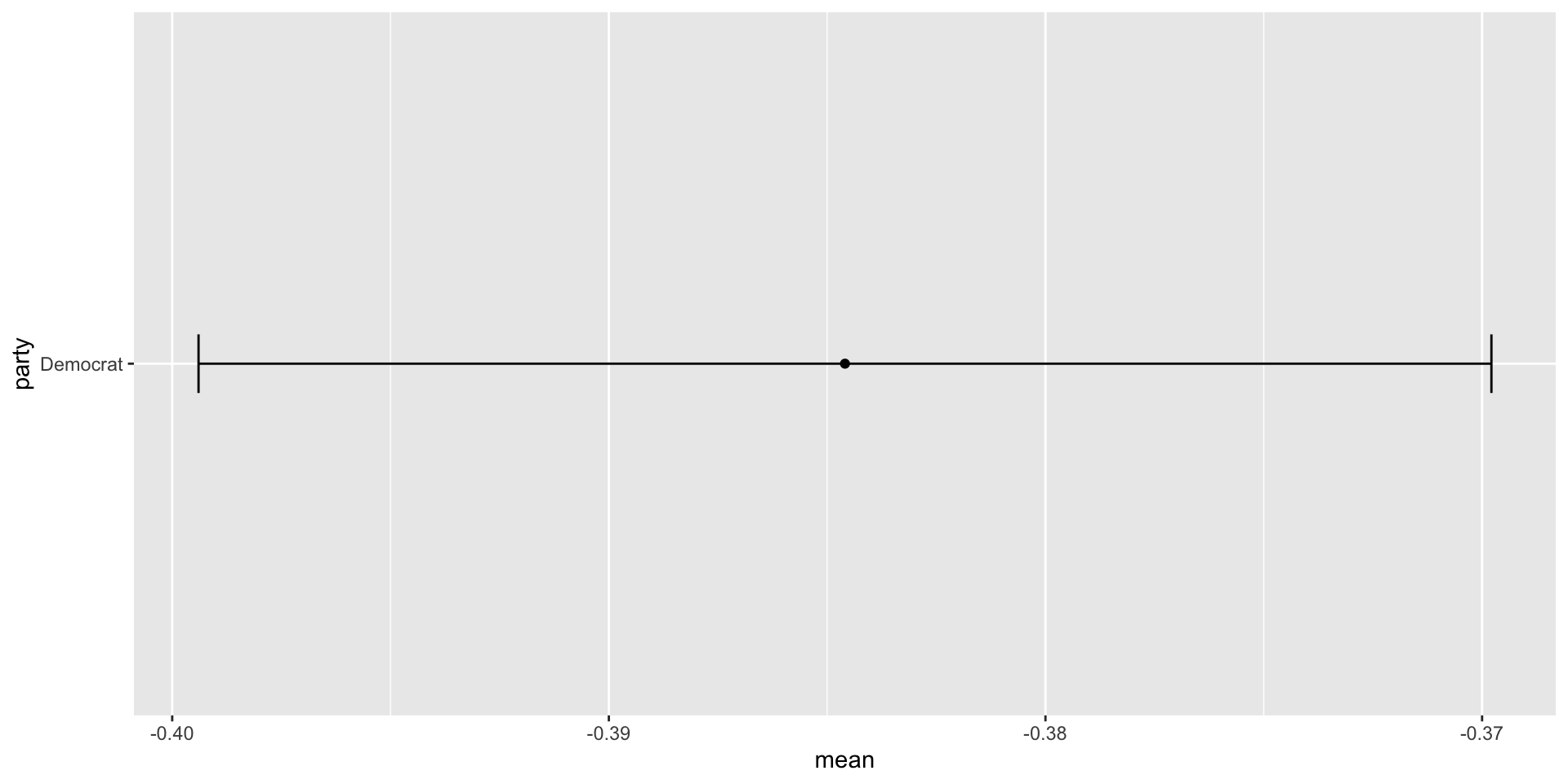
Confidence Intervals: Example

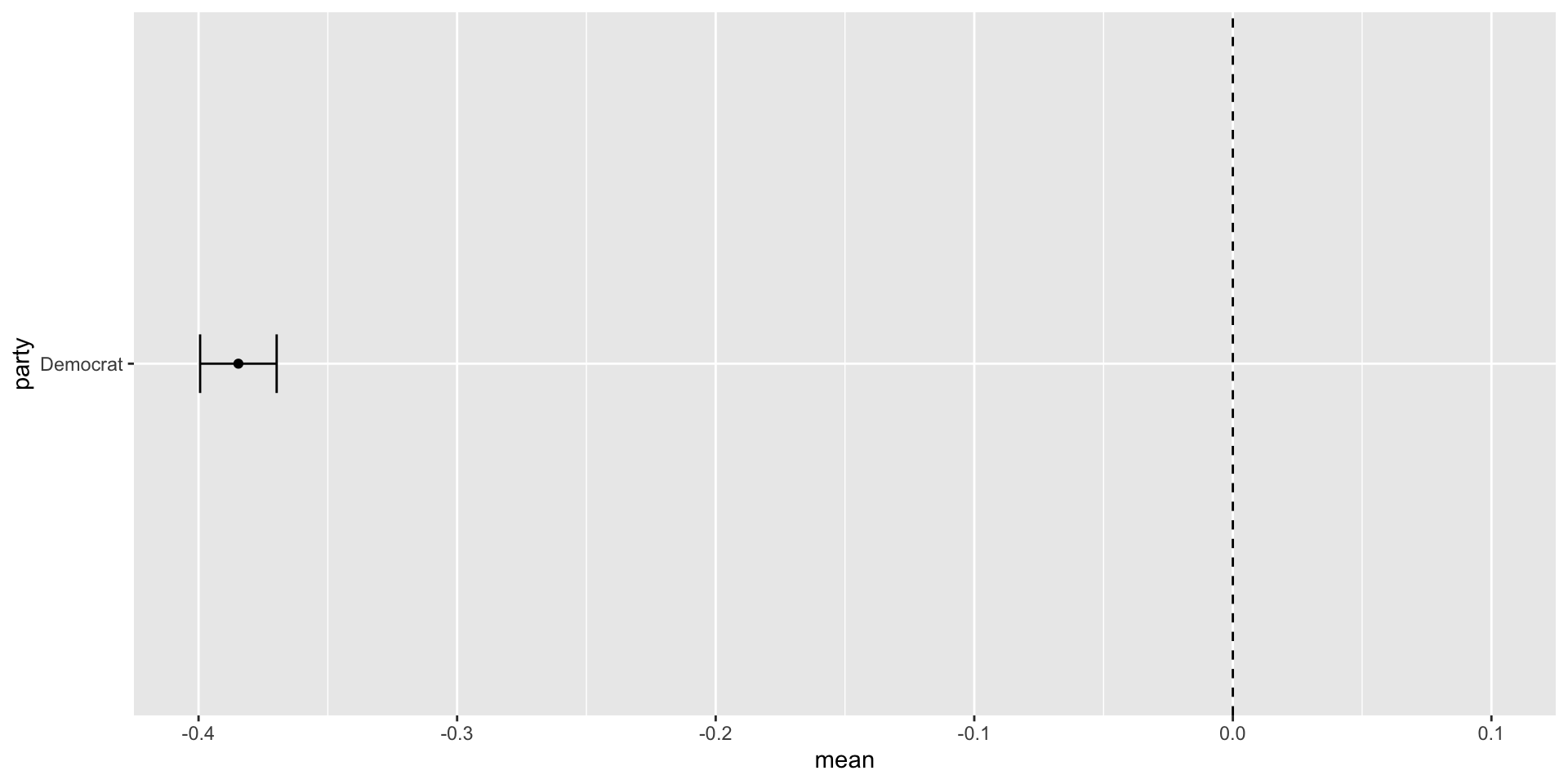
Confidence Intervals

• Most common: 95% “Confidence Intervals”
  • Does NOT mean we are 95% confident that the true population value is in the interval

• Real meaning: if we repeat the sampling process 100 times, 95% of the 95% confidence intervals will contain the true population value (on average)

Confidence Intervals

set.seed(123)
n <- 100000
pop <- rnorm(n, 15, 10)
samp <- sample(pop, size = 100)
samp_mean <- mean(samp)
lb <- samp_mean - qnorm(0.975, mean = 0, sd = 1)*sd(samp)/sqrt(100)
ub <- samp_mean +qnorm(0.975, mean= 0, sd = 1)*sd(samp)/sqrt(100)

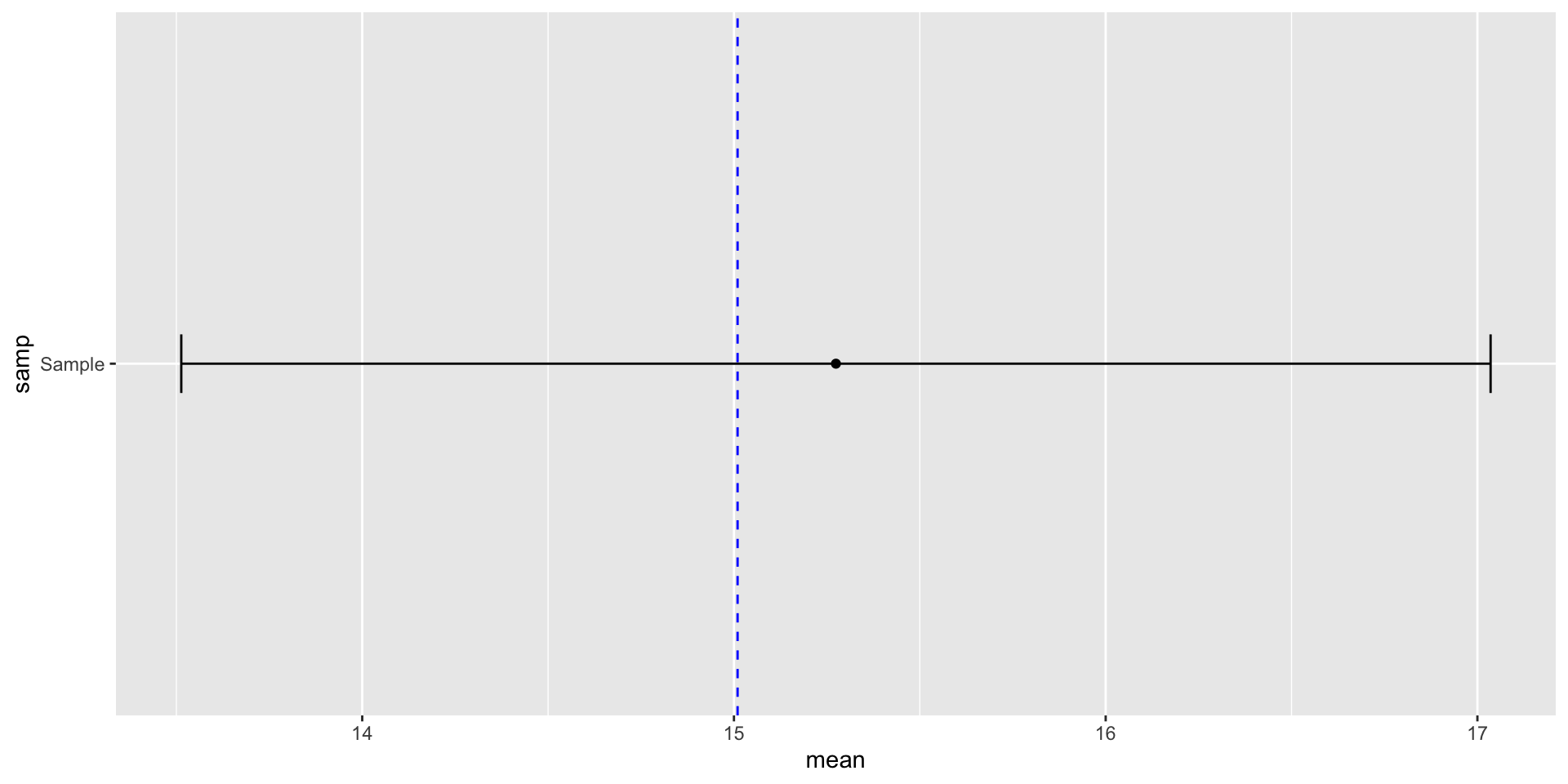
Confidence Intervals

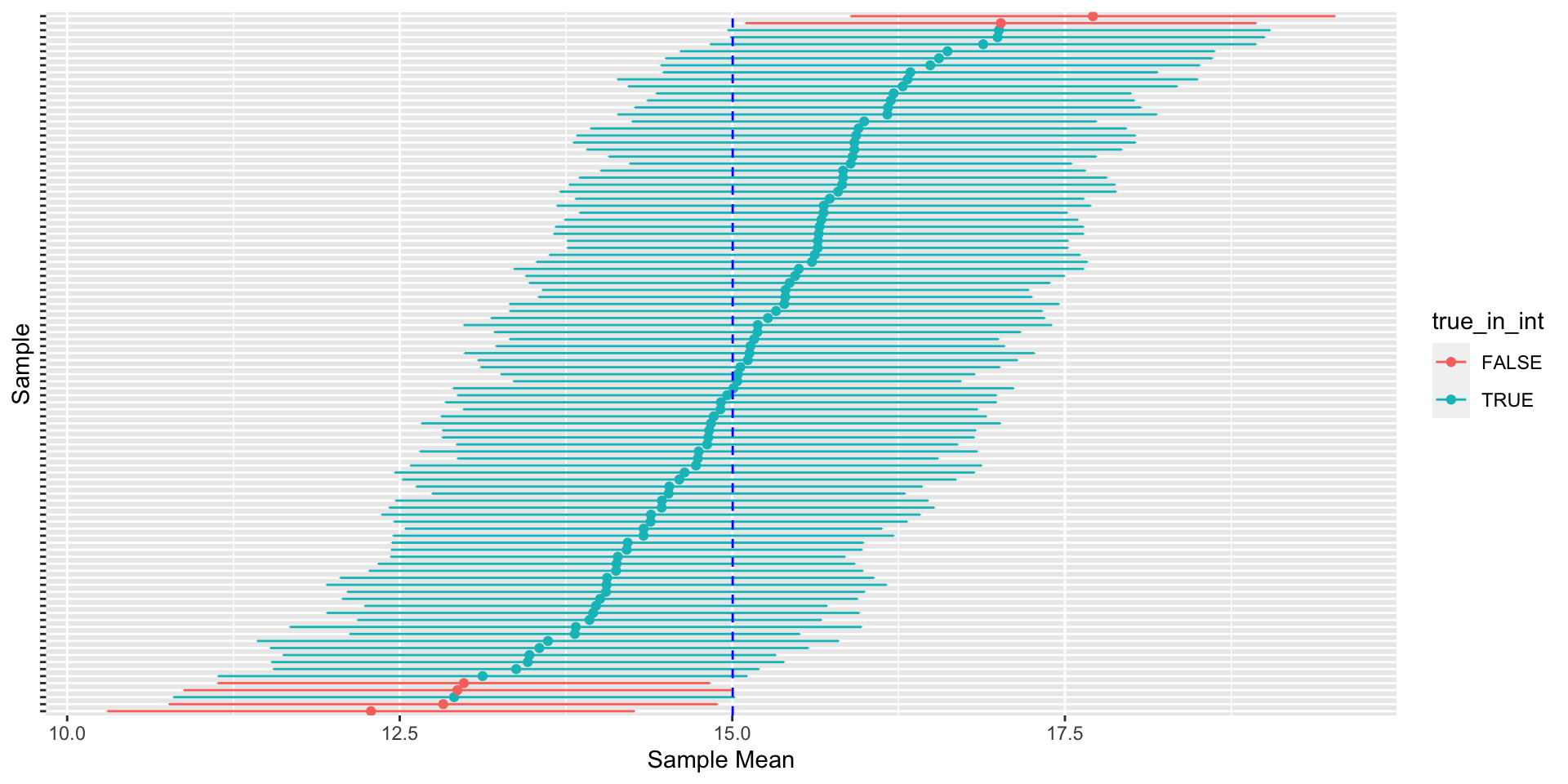
Recap

• Central Limit Theorem (and Law of Large Numbers) central to many scientific tasks

• Used for calculating p-values, hypothesis testing, and constructing confidence intervals

• p-value: probability of observing a Z-score/t-statistic at least as large as the one actually observed if the null hypothesis is true

Recap

• Confidence Intervals:
  • lower bound: sample estimate - \(qnorm(0.975)*\)Standard Error
  • upper bound: sample estimate + \(qnorm(0.975)*\)Standard Error
• We are NOT 95% confident that the true population value is in the interval
  • Only that, if we repeated the sampling process many times, roughly 95% of the intervals would contain the true population mean